Debian-Projektleiterwahlen 2007
Zeitrahmen
| Nominierungsperiode | 4. Februar 2007, 00:00:01 UTC | 25. Februar 2007, 00:00:00 UTC |
|---|---|---|
| Wahlkampfperiode: | 25. Februar 2007, 00:00:01 UTC | 10. März 2007, 00:00:00 UTC |
| Abstimmungsperiode: | 18. März 2007, 00:00:01 UTC | 8. April 2007, 00:00:00 UTC |
Bitte beachten Sie, dass die neue Amtszeit für den Projektleiter am 17. April 2007 beginnt.
Nominationen
- Wouter Verhelst [wouter@debian.org] [Plattform]
- Aigars Mahinovs [aigarius@debian.org] [Plattform]
- Gustavo Franco [stratus@debian.org] [Plattform]
- Sam Hocevar [sho@debian.org] [Plattform]
- Steve McIntyre [93sam@debian.org] [Plattform]
- Raphaël Hertzog [hertzog@debian.org] [Plattform]
- Anthony Towns [ajt@debian.org] [Plattform]
- Simon Richter [sjr@debian.org] [Plattform]
Wenn es soweit ist, kann der Stimmzettel
per E-Mail an
ballot@vote.debian.org
mit dem Betreff leader2007
angefordert werden.
Debatte
Don Armstrong und David Nusinow haben sich bereit erklärt, die Moderatoren der Debatte zu sein. Eine Niederschrift der Debatte ist zum Nachlesen verfügbar.
Daten und Statistiken
Dieses Jahr werden wie immer periodisch während der Wahlperiode Statistiken über die empfangenen Stimmen und die versandten Bestätigungen gesammelt. Zusätzlich wird die Liste der Abstimmenden veröffentlicht. Auch kann die Strichliste angeschaut werden. Bitte beachten Sie, dass die Wahl des Projektleiters einen geheimen Stimmzettel hat, so dass die Strichliste mit dem Hash des Aliases des Wählenden statt dessen Namen erstellt wird; der Alias wird dem Wähler zusammen mit der Bestätigung des Wahlzettels übersandt, so dass jeder überprüfen kann, ob seine Stimme korrekt eingetragen wurde. Während des Urnengangs handelt es sich um eine Pseudo-Strichliste; die endgültige Strichliste wird nach Abschluss des Urnengangs veröffentlicht. Bitte beachten Sie, dass für geheime Abstimmungen die MD5-Prüfsumme in der Pseudo-Strichliste zufällig generiert wird, da andernfalls die Pseudo-Strichliste Informationen über den MD5-Hash und den Wähler durchsickern lassen könnte.
Mindestanzahl
Mit der aktuellen Liste von stimmberechtigten Entwicklern haben wir:
Aktuelle Entwickler-Anzahl = 1036
Q ( sqrt(#devel) / 2 ) = 16,0934769394311
K min(5, Q ) = 5
Quorum (3 x Q ) = 48,2804308182932
Quorum
- Option 1 erreichte Quorum: 337 > 48,2804308182932
- Option 2 erreichte Quorum: 142 > 48,2804308182932
- Option 3 erreichte Quorum: 268 > 48,2804308182932
- Option 4 erreichte Quorum: 346 > 48,2804308182932
- Option 5 erreichte Quorum: 342 > 48,2804308182932
- Option 6 erreichte Quorum: 340 > 48,2804308182932
- Option 7 erreichte Quorum: 298 > 48,2804308182932
- Option 8 erreichte Quorum: 183 > 48,2804308182932
Mehrheitsanforderung
Alle Kandidaten benötigten eine einfache Mehrheit, um wählbar zu sein.
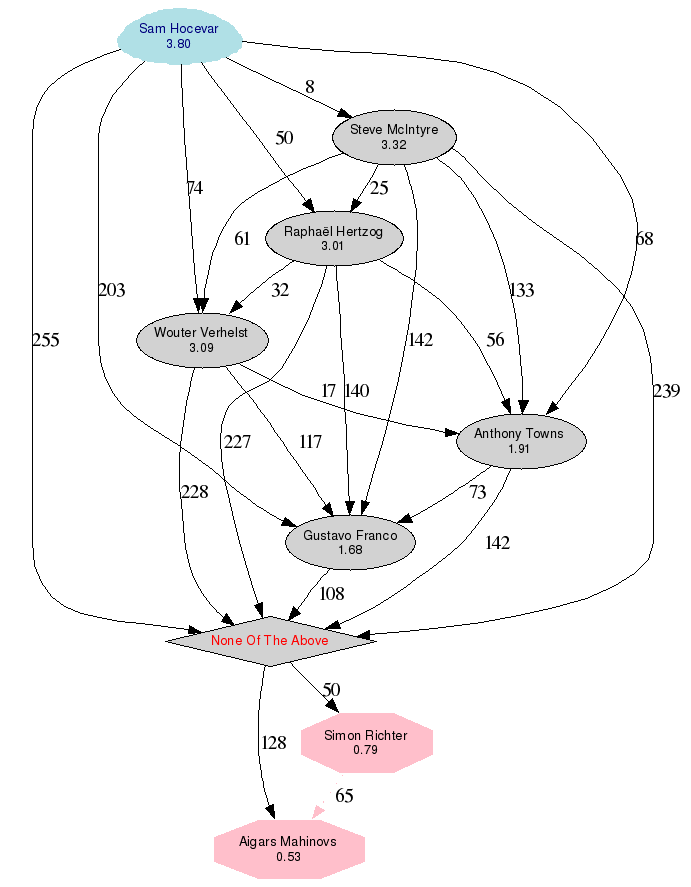
Ergebnis
In der obigen Graphik implizieren die rosa gefärbte Knoten jene, die nicht die Mehrheit erlangten, der blaue ist der Gewinner. Das Achteck wird für die Optionen verwendet, die nicht den Standard geschlagen haben.
- Option 1
Wouter Verhelst
- Option 2
Aigars Mahinovs
- Option 3
Gustavo Franco
- Option 4
Sam Hocevar
- Option 5
Steve McIntyre
- Option 6
Raphaël Hertzog
- Option 7
Anthony Towns
- Option 8
Simon Richter
- Option 9
Keiner der Obigen
In der folgenden Tabelle repräsentiert tally[Zeile x][Spalte y] die Stimmen, die Option x über Option y erhalten hat. Eine detailliertere Erklärung der Sieg-Matrix kann Ihnen beim Verständnis der Tabelle helfen. Zum Verständnis der Condorcet-Methode ist der Wikipedia-Eintrag recht informativ.
| Option | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Option 1 | 340 | 247 | 163 | 163 | 181 | 219 | 331 | 337 | |
| Option 2 | 28 | 38 | 31 | 45 | 37 | 91 | 94 | 142 | |
| Option 3 | 130 | 255 | 75 | 129 | 121 | 170 | 239 | 268 | |
| Option 4 | 237 | 329 | 278 | 211 | 227 | 252 | 330 | 346 | |
| Option 5 | 224 | 344 | 271 | 203 | 215 | 264 | 330 | 342 | |
| Option 6 | 213 | 342 | 261 | 177 | 190 | 240 | 326 | 340 | |
| Option 7 | 202 | 307 | 243 | 184 | 131 | 184 | 287 | 298 | |
| Option 8 | 42 | 159 | 73 | 43 | 58 | 56 | 109 | 183 | |
| Option 9 | 109 | 270 | 160 | 91 | 103 | 113 | 156 | 233 | |
Wie in Zeile 2, Spalte 1 sichtbar, erhielt Aigars Mahinovs
28 Stimmen gegenüber Wouter Verhelst
Wie in Zeile 1, Spalte 2 sichtbar, erhielt Wouter Verhelst
340 Stimmen gegenüber Aigars Mahinovs.
Paarweise Niederlagen
- Option 1 besiegt Option 3 mit ( 247 - 130) = 117 Stimmen.
- Option 4 besiegt Option 1 mit ( 237 - 163) = 74 Stimmen.
- Option 5 besiegt Option 1 mit ( 224 - 163) = 61 Stimmen.
- Option 6 besiegt Option 1 mit ( 213 - 181) = 32 Stimmen.
- Option 1 besiegt Option 7 mit ( 219 - 202) = 17 Stimmen.
- Option 1 besiegt Option 9 mit ( 337 - 109) = 228 Stimmen.
- Option 4 besiegt Option 3 mit ( 278 - 75) = 203 Stimmen.
- Option 5 besiegt Option 3 mit ( 271 - 129) = 142 Stimmen.
- Option 6 besiegt Option 3 mit ( 261 - 121) = 140 Stimmen.
- Option 7 besiegt Option 3 mit ( 243 - 170) = 73 Stimmen.
- Option 3 besiegt Option 9 mit ( 268 - 160) = 108 Stimmen.
- Option 4 besiegt Option 5 mit ( 211 - 203) = 8 Stimmen.
- Option 4 besiegt Option 6 mit ( 227 - 177) = 50 Stimmen.
- Option 4 besiegt Option 7 mit ( 252 - 184) = 68 Stimmen.
- Option 4 besiegt Option 9 mit ( 346 - 91) = 255 Stimmen.
- Option 5 besiegt Option 6 mit ( 215 - 190) = 25 Stimmen.
- Option 5 besiegt Option 7 mit ( 264 - 131) = 133 Stimmen.
- Option 5 besiegt Option 9 mit ( 342 - 103) = 239 Stimmen.
- Option 6 besiegt Option 7 mit ( 240 - 184) = 56 Stimmen.
- Option 6 besiegt Option 9 mit ( 340 - 113) = 227 Stimmen.
- Option 7 besiegt Option 9 mit ( 298 - 156) = 142 Stimmen.
Die Schwartz-Menge enthält
- Option 4
Sam Hocevar
Der Gewinner
- Option 4
Sam Hocevar
Debian benutzt die Condorcet-Methode für Abstimmungen.
Vereinfachend kann die grundlegende
Condorcet-Methode folgendermaßen beschrieben werden:
Ziehe alle möglichen Zweikämpfe zwischen den Kandidaten
in Betracht. Der Condorcet-Gewinner, wenn es einen gibt,
ist derjenige Kandidat, der jeden anderen Kandidaten im
Zweikampf schlagen kann.
Das Problem ist, dass es bei komplexen Wahlen durchaus zu
einer kreisförmigen Beziehung kommen kann, in der A über
B siegt, B über C siegt und C über A siegt. Die meisten
Variationen von Condorcet verwenden verschiedene Mittel,
um diese Pattsituation aufzulösen. Siehe
Cloneproof Schwartz Sequential Dropping
für Details.
Die Variation von Debian ist in
der Satzung
schriftlich festgehalten, speziell § A.6.
Manoj Srivastava