Debian Project Leader Elections 2007

Time Line

Nomination period: February 4th 00:00:01 UTC, 2007 February 25th 00:00:00 UTC, 2007
Campaigning period: February 25th 00:00:01 UTC, 2007 March 18th 00:00:00 UTC, 2007
Voting period: March 18th, 00:00:01 UTC, 2007 April 8th, 00:00:00 UTC, 2007

Please note that the new term for the project leader shall start on April 17th, 2007.

Nominations

  1. Wouter Verhelst [wouter@debian.org] [platform]
  2. Aigars Mahinovs [aigarius@debian.org] [platform]
  3. Gustavo Franco [stratus@debian.org] [platform]
  4. Sam Hocevar [sho@debian.org] [platform]
  5. Steve McIntyre [93sam@debian.org] [platform]
  6. Raphaël Hertzog [hertzog@debian.org] [platform]
  7. Anthony Towns [ajt@debian.org] [platform]
  8. Simon Richter [sjr@debian.org] [platform]

The ballot, when ready, can be requested through email by emailing ballot@vote.debian.org with the subject leader2007.

Debate

Don Armstrong and David Nusinow have volunteered to be a debate moderator. A transcript of the debate is available for review.

Data and Statistics

This year, like always, statistics are being gathered about ballots received and acknowledgements sent periodically during the voting period. Additionally, the list of voters will be recorded. Also, the tally sheet will also be made available to be viewed. Please remember that the project leader election has a secret ballot, so the tally sheet will be produced with the hash of the alias of the voter rather than the name; the alias shall be sent to the corresponding voter along with the acknowledgement of the ballot so that people may verify that their votes were correctly tabulated. While the voting is open the tally will be a dummy one; after the vote, the final tally sheet will be put in place. Please note that for secret ballots the md5sum on the dummy tally sheet is randomly generated, as otherwise the dummy tally sheet would leak information relating the md5 hash and the voter.

Quorum

With the current list of voting developers, we have: 

 Current Developer Count = 1036
 Q ( sqrt(#devel) / 2 ) = 16.0934769394311
 K min(5, Q )           = 5
 Quorum  (3 x Q )       = 48.2804308182932

Quorum

Majority Requirement

All candidates would need a simple majority to be eligible.

 

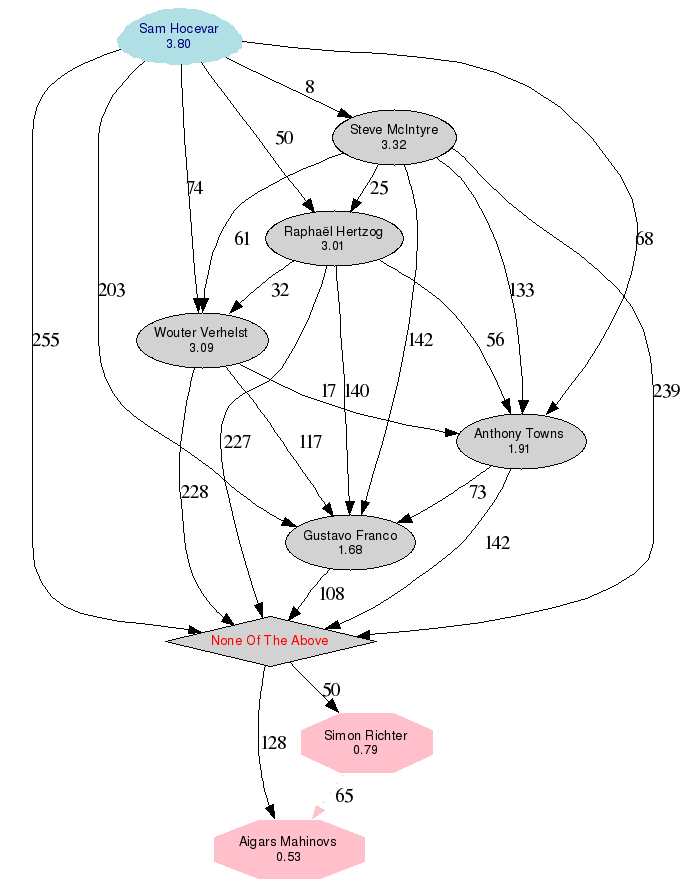
Outcome

Graphical rendering of the results

In the graph above, any pink colored nodes imply that the option did not pass majority, the Blue is the winner. The Octagon is used for the options that did not beat the default.

In the following table, tally[row x][col y] represents the votes that option x received over option y. A more detailed explanation of the beat matrix may help in understanding the table. For understanding the Condorcet method, the Wikipedia entry is fairly informative.

The Beat Matrix
 Option
  1 2 3 4 5 6 7 8 9
Option 1   340 247 163 163 181 219 331 337
Option 2 28   38 31 45 37 91 94 142
Option 3 130 255   75 129 121 170 239 268
Option 4 237 329 278   211 227 252 330 346
Option 5 224 344 271 203   215 264 330 342
Option 6 213 342 261 177 190   240 326 340
Option 7 202 307 243 184 131 184   287 298
Option 8 42 159 73 43 58 56 109   183
Option 9 109 270 160 91 103 113 156 233  

Looking at row 2, column 1, Aigars Mahinovs
received 28 votes over Wouter Verhelst

Looking at row 1, column 2, Wouter Verhelst
received 340 votes over Aigars Mahinovs.

Pair-wise defeats

The Schwartz Set contains

The winners

Debian uses the Condorcet method for voting. Simplistically, plain Condorcets method can be stated like so :
Consider all possible two-way races between candidates. The Condorcet winner, if there is one, is the one candidate who can beat each other candidate in a two-way race with that candidate. The problem is that in complex elections, there may well be a circular relationship in which A beats B, B beats C, and C beats A. Most of the variations on Condorcet use various means of resolving the tie. See Cloneproof Schwartz Sequential Dropping for details. Debian's variation is spelled out in the constitution, specifically, A.6.

Manoj Srivastava